简介

正如 Wiki 中对最大似然估计的描述：

在概率统计中，最大似然估计是用来估计一个概率模型的参数的一种方法。

接下来，我们将从二项分布开始讲起。

假设，我们有个样本集：{0，1， 1， 0， 1， 1}其中样本集中不同数字对应的概率如下： $$p(x = 1) = \mu, p(x = 0) = 1-\mu$$

那么对应参数 $\mu$ 的最大似然是什么呢？

我们可以将该样本集想象成投掷硬币的结果集，其中 1 表示正面，0 表示反面。从样本集看，投掷硬币的结果更偏向硬币的正面，但是有多大概率投掷的结果是正面呢？

让我们将每次投掷结果对应的概率相乘，并得到一个 $\mu$ 的函数: $$L(\mu) = p(0)p(1)p(1)p(0)p(1)p(1) = (1-\mu)\mu \mu(1-\mu)\mu \mu = (1-\mu)^{2}\mu^{4}$$

那么对 $L(\mu)$ 做对数变换： $$log(L(\mu)) = 2log(1-\mu) + 4log(\mu)$$

在最大化$L(\mu)$的基础上，计算出 $\mu$ 对应的值。 那么我们可以计算 $log(L(\mu))$ 对 $\mu$ 的导数 $$(log(L))^{'} = \frac{-2}{1-\mu} + \frac{4}{\mu} = 0$$

从而 $\mu = 2/3$.

但是，我们并不确定 $\mu = 2/3$ 是最大值点，还是鞍点。所以我们通过计算 $log(L)$ 的二阶导来确定下: $$(logL)^{''} = \frac{2}{(1-\mu)^{2}} - \frac{4}{\mu^{2}}$$

我们将 $\mu = 2/3$ 带入上式得到的结果值是一个负数，所以 $\mu = 2/3$ 是函数 $log(L)$ 对应的最大值。

因此如果该样本集是投掷硬币的结果集，那么我们可以说投掷硬币有 $2/3$ 的概率得到正面。

上述例子只包含一个参数($\mu$)。

下面将介绍个更广泛的模型，用于估计多个参数的方法。

极大似然估计(MLE)

让我们看下下面的极大似然函数：

$L(w) = \prod^{n}_{i} (\phi(z^{(i)})^{y^{(i)}}(1-\phi(z^{(i)}))^{y^{(i)}})$ （1）

与上节中的似然函数 $L(\mu)$ 相比，公式（1）中的 $\phi(z)$ 就是对应的概率： $$\phi(z) = p(y=1|x;w) = \frac{1}{1+e^{-z}}$$

其中$z$ 是如下输入: $$z = \sum_{i}w_{i}x_{i}$$

正如公式所示，使用逻辑回归去估计对应,样本的类别和相应的概率。

现在让我们来看下该模型对应的参数，如上定义的权重 $w$ 对应的似然函数 $L(w)$。 当我们构建逻辑回归模型时，我们希望最大化似然函数。

换句话说，最大化似然函数就是最大化相应的概率值。但我们经常说的是损失，对极大似然函数取反作为损失函数 $J$

为了方便，我们可以将似然函数作为我们的损失函数。$J(w)$， 这样我们就可以使用梯度下降法进行相应的优化。 $$log(L(w)) = \sum^{n}_{i}y^{(i)}log(\phi(z^{(i)})) + (1-y^{(i)})log(1-\phi(z^{(i)}))$$ $$J(w) = \sum^{n}_{i}-y^{(i)}log(\phi(z^{(i)})) - (1-y^{(i)})log(1-\phi(z^{(i)}))$$

为了让我们更清晰的了解该损失函数，我们来看只有一个样本的损失函数： $$J(\phi(z), y; w) = \sum^{n}_{i}-ylog\phi(z) - (1-y)log(1-\phi(z))$$

如果我们仔细看下这个等式，当 $y=0$ 时等式的第一项就消失了，当 $y = 1$时等式的第二项就消失了。正如下图所示： $$J(\phi(z), y; w) = -log(\phi(z)) \quad if \quad y = 1$$ $$J(\phi(z), y; w) = -log(1-\phi(z)) \quad if \quad y = 0$$

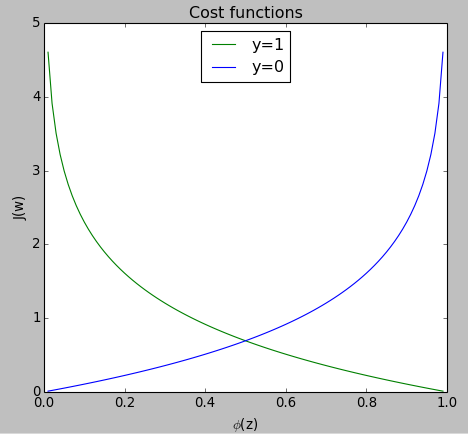
如图所示，我们可以看到当我们正确的预测一个样本的标签为 $y = 1$ 时损失函数的值接近于 0 （绿色曲线）。 从 $y$ 轴看，但标签 $y=0$ 时损失函数的值接近于 0（蓝色）。

图片对应的代码:

import matplotlib.pyplot as plt
import numpy as np

phi = np.arange(0.01, 1.0, 0.01)
j1 = -np.log(phi)
j0 = -np.log(1-phi)
plt.plot(phi, j1, color="green", label="y=1")
plt.plot(phi, j0, color="blue", label="y=0")

plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.title('Cost functions')
plt.grid(False)
plt.legend(loc='upper center')
plt.show()