简介
最优化往往都是我们最求的最终目标,不管是在解决生活中的问题或者是构建一个软件产品。最优化最基本的要求就是寻找问题的最优解。如果你阅读了这篇与最优化相关的文章, 你会发现最优化理论在我们生活中扮演了非常重要的角色。
不过最优化在机器学习的应用与在别的领域上的应用有一些不太一样的地方。总的来说,在我们寻找最优时,我们通常知道数据的分布情况,并且知道需要对哪些地方做优化。但是在机器学习中,我们并不太了解输入的新数据是怎样的数据。
最优化理论的广泛应用
目前有很多最优化理论被应用到了不同的领域,例如:
- 机械学(Mechanics): 例如,如何设计最优的航天航空器械的表面
- 经济学(Economics): 例如,最小化损失
- 物理学(Physis): 例如:量子计算中的时间优化
最优化理论还在其他很多领域上得到了重要的应用,比如,选择最优的运输路径,货架空间优化等待。
同样,最优化理论也在很多机器学习算法中得到了应用,例如:线性回归,k-最近邻,神经网络等等。最优化的应用不管是在研究领域还是工业上都得到了广泛的研究和应用。
在这篇文章中,我们主要关注其中一个最优化算法,梯度下降法(Gradient Descent)。该算法在机器学习领域得到了比较广泛的应用。
目录
1. 什么是梯度下降
在现实生活中,从山顶走到山脚很好很形象的展示了梯度下降的过程
假设你在山顶,你想走到山脚下的湖边。有一个限制就是你眼睛被蒙着,看不到你前进的方向。在这情况下,该如何走到山脚下的湖边?

最好的方法就是不断尝试寻找身边向下走的道路。这样能告诉你应该向什么方向走出新的一步。如果你延着向下的道路方向,那么你就很可能可以走到山脚下的湖边。正如下图所示:
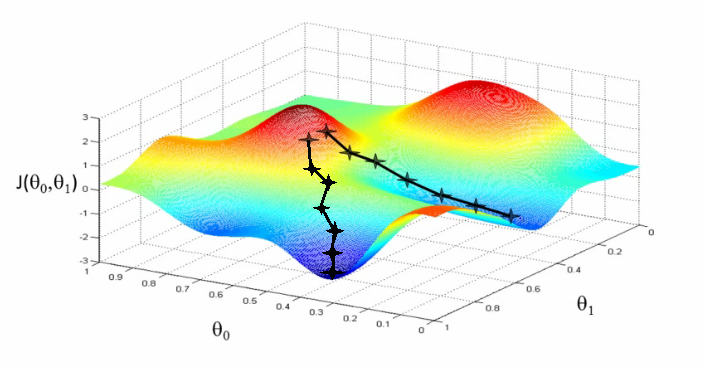
接下来,让我们将图上直观的认识转换成数学上的解释,从而得到理论上的支持。
假设我们想为我们的学习算法找到最优的参数 和 。 更上面的分析一样,当我们把损失函数空间(Cost Space)画出来也能找到想到相同的山顶和山脚。损失函数空间(Cost Space)就是当我们选择某一特定值时,我们的算法最终计算出来的结果。
因此,在上图y轴是选的特定参数 和 对应的损失 , 其中 和 分别对应着图中的x轴和z轴。 在这,红色部分表示山顶,对应着高损失。 蓝色部分表示山脚,对应着低损失。
到目前为止,有很多样式的梯度下降算法。它们可以按照两种不同的方式进行分类。
- 根据数据数据的多少
- 全量梯度下降算法(Full Batch Gradient Descent Algorithm)
- 随机梯度下降算法(Stochastic Gradient Descent Algorithm )
在全量梯度下降算法中,每次训练都使用的是全量的数据来计算梯度。对于随机梯度下降算法,每次训练使用的是一个训练数据来计算梯度。
- 根据不同的微分技术
- 一阶微分(导数)
- 二阶微分(导数)
梯度下降算法需要通过计算损失函数的微分(导数)来计算相应的梯度值。我们可以使用一阶微分(导数),或者二阶微分(导数)。
2. 应用梯度下降算法时的一些挑战
虽然梯度下降法在非常多的领域得到了非常好的应用。但是也存在一些问题,梯度下降算法也许不太合适,甚至容易得到失败的结果。其中以下三种情况下容易造成梯度下降算法出现问题:
- 数据挑战(Data Challenges)
- 梯度挑战(Gradient Challenges)
- 实现挑战(Implementation Challenges)
2.1 数据挑战(Data Challenges)
- 如果数据呈现出的是非凸优化问题。那么使用梯度下降就无法计算出最优的结果。梯度下降算法只适用于凸优化问题。
- 就是是凸优化问题,也可能出现多个最小值点。其中最小值中最小的点被称为全局最小点,其他非全局最小点被称为局部最小点。我们的最终目的是规避局部最小点,来寻找全局最小点。
- 同样我们也会遇到鞍点(saddle points), 鞍点的梯度也等于零,但它并不是最优点。我们没有什么很好的办法来规避鞍点,目前这还是一个值得研究的领域。
2.2 梯度挑战(Gradient Challenges)
- 如果在执行梯度下降时不正确,则可能会导致梯度消失或者梯度爆炸的问题。这种问题通常是因为梯度太小或者太大,导致整个算法无法收敛。
2.3 实现挑战(Implementation Challenges)
- 有很多神经网络实践者,在实现相应算法时,没有很好的考虑到计算资源的分配和利用。例如:在实现梯度下降算法时,对于算法在计算过程中需要使用多少资源是很重要的。假设对于应用来说计算内存太小,最终容易导致整个网络的失败。
- 还有就是关注浮点数和硬件/软件的先决条件
3. 不同类型的梯度下降算法
让我们来看下几种比较常用的梯度下降算法以及他们的实现。
3.1 Vanilla Gradient Descent
这是最简单的梯度下降算法。这边的 Vanilla 表示的是最纯粹不带任何修改的意思。其主要特点是通过计算损失函数的梯度向最小值方向移动一小步。
让我们看下相应的伪代码
update = learning_rate * gradient_of_parameters
parameters = parameters - update
从上面的伪代码我们可以看出,我们通过计算参数对应的梯度同时乘以相应的学习率(learning_rate) 来对变量进行更新。其中学习率(learning_rate)是一个控制我们能多快获取到最小值的参数值。学习率(learning_rate)是一个超参数(hyper-parameter), 我们在选择学习率时需要非常的小心。
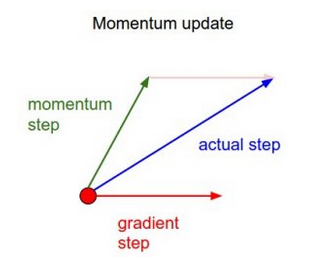
3.2 Gradient Descent with Momentum
在Gradient Descent with Momentum 算法中,主要是对上述算法做了一些改变,其中主要是在计算下一步参数变化时加入了上一步参数变化的信息。
对应的伪代码
update = learning_rate * gradient
velocity = previous_update * momentum
parameter = parameter + velocity – update
该算法与上述的 vanilla 梯度下降比较类似。但是引入了一个新元素就是velocity(速率),该值包含了对前一步更新的考虑,同时增加了一个常量 momentum。
3.3 ADAGRAD
ADAGRAD采用了自适应的方式对学习率(learning rate)进行更新。在这个算法中,根据以前所有迭代的梯度变化情况,我们尝试改变学习速率。
对应的伪代码
grad_component = previous_grad_component + (gradient * gradient)
rate_change = square_root(grad_component) + epsilon
adapted_learning_rate = learning_rate * rate_change
update = adapted_learning_rate * gradient
parameter = parameter – update
在上面的代码中,epsilon是一个常量,用于保持学习速率的变化率。
3.4 ADAM
ADAM 是在 ADAGRAD的基础上做了进一步的改进自适应算法。从另一个角度,你可以认为是 Momentum 加 ADAGRAD算法的综合。
对应的伪代码
adapted_gradient = previous_gradient + ((gradient – previous_gradient) * (1 – beta1))
gradient_component = (gradient_change – previous_learning_rate)
adapted_learning_rate = previous_learning_rate + (gradient_component * (1 – beta2))
update = adapted_learning_rate * adapted_gradient
parameter = parameter – update
在这里,beta1和beta2是常量,用于控制梯度和学习速率的变化。
这里同样还有基于二阶导数的算法,比如:l-BFGS,你可以在 scipy library 找到相应的实现。
4. 梯度下降算法使用小技巧
上述的梯度下降算法都有相应的优点和缺点。这里会简单介绍一些小技巧,主要是帮助各位能更方便的选择合适的算法。
- 为了能快速的计算,请采用自适应算法,比如:Adam和Adagrad。它们能帮助你在花费更小的代价的前提下能更快的获取结果,同时也不需要设定太多的超参数(hyper-parameters)。
- 为了得到更好的结果,大家应该使用 vanilla 或者 momentum梯度下降算法。虽然它们相比自适应算法获取结果的速度更慢,但是结果会更好。
- 如果你的训练数据非常少,并且能在一次迭代后被很好的拟合。那么可以采用二阶导数技术,例如:l-BFGS。主要因为二阶导数不仅非常的快收敛,同时结果也比较准确。但是仅仅适用于数据量比较少的时候。
- 还有一种比较新兴的梯度下降算法,就是采用训练特征来估计学习率(learning rate)。若感兴趣的可以看看这篇文章
导致神经网络训练失败的原因有很多,但是如果你能知道你算法在哪出错,或者不适用将是非常有帮助的。
在应用梯度下降算法时,你可以通过以下几点来帮助你规避一些问题:
- 错误率(Error rate): 你应该在几次参数迭代后计算下相应的训练和测试错误率,保证它们都是在降低的。如果不是,那么可能就有问题了。
- 网络隐藏层Gradient flow: 检查网络保证梯度下降不会出现梯度消失或者梯度爆炸的问题。
- 学习率(learning rate): 在使用自适应算法时,你需要保持对学习率的检查。
5. 其他资源
- 文章资源,An overview of gradient descent optimization algorithms
- 在线课程资料, CS231n 关于梯度下降的在线课程资料
- Deep Learning Book 第四章,数值优化, 第八章 深度模型的最优化