Haiyang Wang

Stay hungry, Stay foolish

循环神经网络(RNN)简介(译)

08 Dec 2017 » deeplearning, machine-learning

简介

让我们通过一个例子来展开本文— “working love learning we on deep”，你能看这句话的意思？不能，那换一句再看看 “We love working on deep learning”。这句话的意思就显而易见了。简单的调换句子中词的顺序就让句子就不连贯了。那么，我们能期待一个神经网络理解这类句子？并不能，如果人脑都很难理解这类句子，我想神经网络也很难破译这类句子。

在现实生活中，存在很多类似的因为顺序打乱而导致整体的意思招到了破坏。例如，我们前面说的单词序列定义了它们的含义，就是所谓的时间序列，不同时间序列的事件，基因组序列数据，其中不同序列拥有不同的含义。在多数情况下，其中信息的序列决定了事件本身的意义。如果我们需要使用这类序列数据来获得任何有意义的输出结果。我们需要一个能够保留一些数据先前知识的网络来完全定义理解他。循环(递归)神经网络因此发挥了作用。

目录

1. 什么场景需要神经网络处理序列数据

在我们深入了解循环(递归)神经网络之前，让我们思考下，我们在现实生活中我们是否真的需要处理序列信息数据。还有什么样的任务我们可以使用循环(递归)神经网络来处理。

循环(递归)神经网络的优势在于它应用的多样性。如下几个场景RNN具有很强的处理各种输入输出的能力。

  • 情绪分类（Sentiment Classification） 这类任务可以将推文简单的分为表达的积极还是表达的消极情绪。所以输入的是任意长度的推文，则输出就是固定的推文类型。

  • 图像标题(Image Captioning) 假设我们有一张图片，并且希望根据图片的内容提取相应的文字描述信息。因此，我们有一个输入–一张图片，一系列或者一串单词作为输出。在这图片大小有可能是固定的，但是输出的文字长度是不等长的。

  • 语言翻译(Language Translation) 假设我们有一个其他语言的序列文本，例如英文，我们希望将它转换成法文。不同的语言有它特定的语法，所以同一意思的语句再不同的语言中对应的长度也不一致。所以对于该场景，输入和输出的长度都不一致。

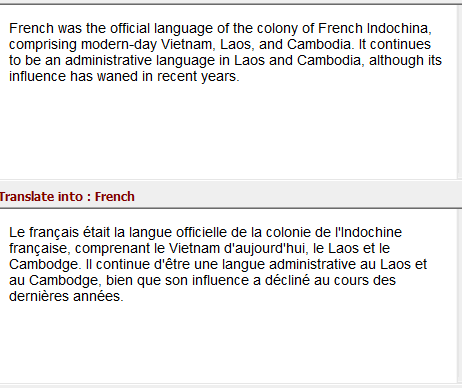
所以RNN可以接收不同样式，长度的输入和输出。接下来我们来具体看下RNN的结构。

2. 什么是循环(递归)神经网络

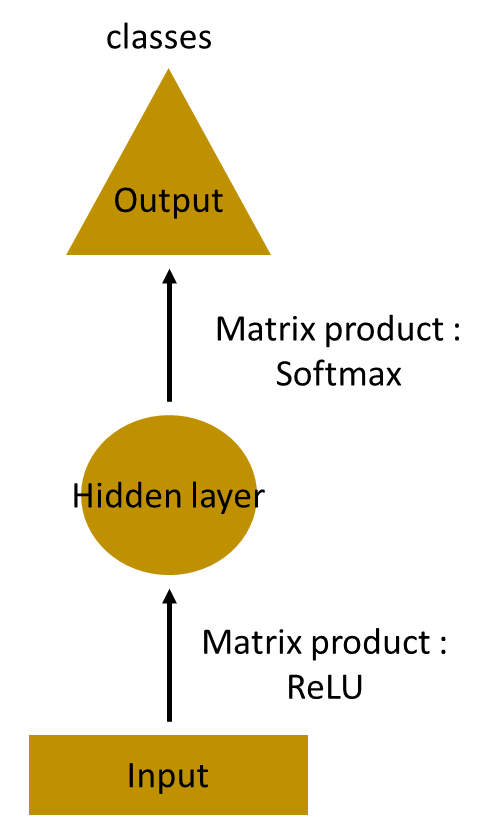
让我们看下用于预测句子中下一个单词的任务。让我们使用MLP来处理这个任务看看，那么在MLP中是怎么操作的。在这个简单的例子中，我们有一个输入层，一个隐藏层，还有一个输出层。输入层获的输入，隐藏层激活，最后通过输出层得到最终的结果。

接下来让我们看下拥有更多层的神经网络（如下图），在这输入层接收输入，通过几层隐藏层的处理后，将隐藏层的输出结果放入输出层得到最终的输出。每一层隐藏层都有他们自己独立的权重和偏移量参数。

因为每一层都有独立的权重和偏移量参数，那么他们之间是相互独立的。接下来我们需要确定连续输入之间的关系，我们同样可以将输入数据直接传入隐藏层。

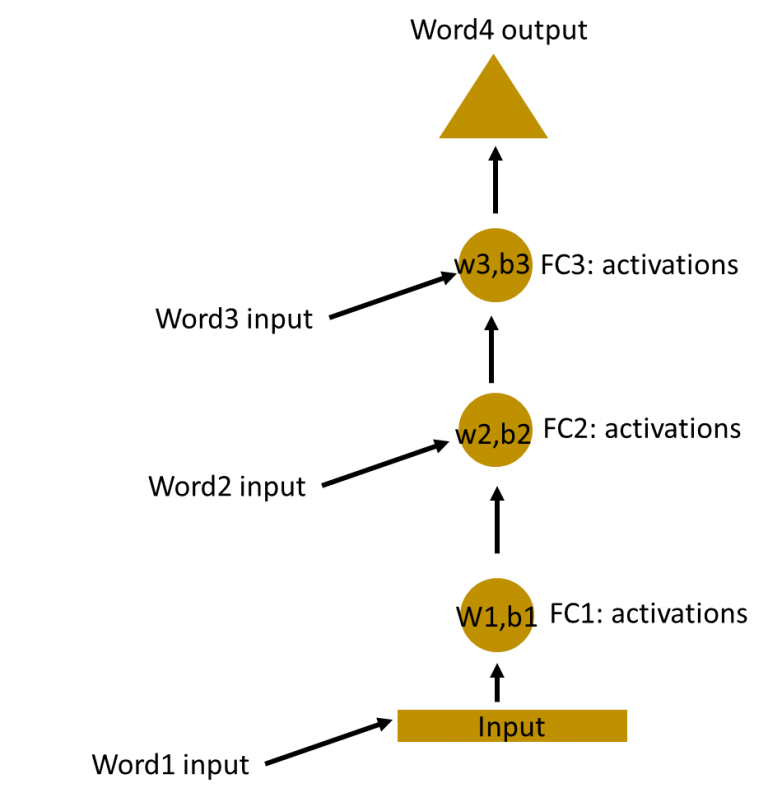
在这，不同隐藏层的权重和偏移量是不同的。同时这些隐藏层是相互独立的所以无法进行合并。若要将隐藏层合并那他们之间的权重和偏移量必须保持一致。

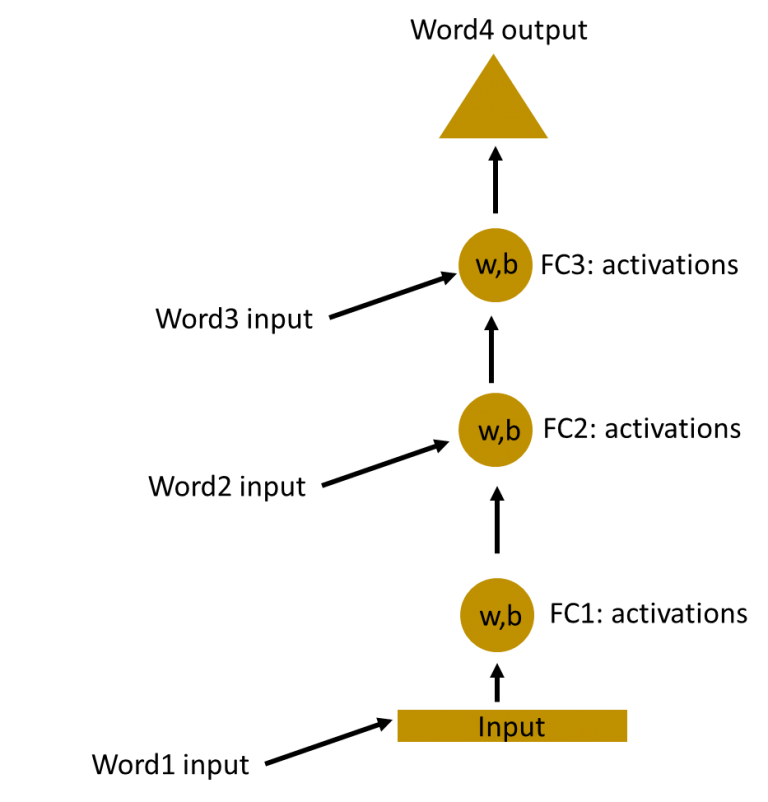
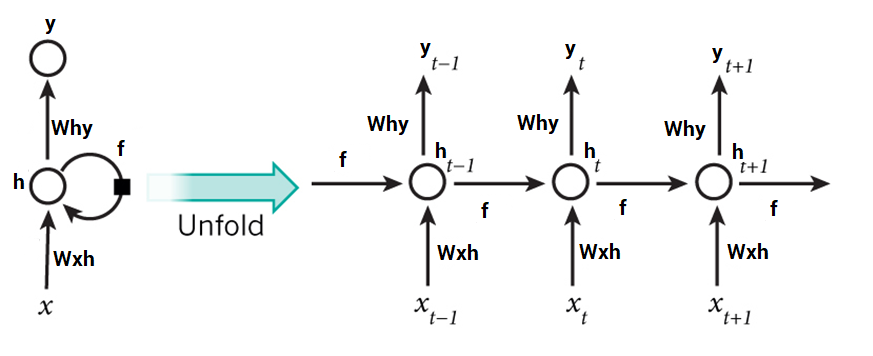
现在我们可以将这些隐藏层给合并，保证他们之间的权重和偏移量都保持一致。所有这些隐藏层可以在一个单独的循环图中一起展开。

这就好比将输入数据直接传入隐藏层。在任何时候循环神经元的权重和偏移量参数都是一样的，因为现在只有一层。因为循环神经元存储了前一输入的状态并且结合了当前输入的状态，某种层度上保留了前一输入和当前输入的关系。

3. 循环(递归)神经网络详解

让我们先看一个简单的例子。让我们看一个字符级别的RNN，假设我们有一个单词 ‘Hello’。我们提供前4个字符 ‘h’，‘e’，‘l’，‘l’ 然后需要神经网络预测出最后一个字符’o’。 所以在这个任务中只包含了4个字符 {‘h’, ‘e’, ‘l’, ‘o’} 。 在实际的自然语言处理中包含了整个维基百科中包含的所有词汇，或者某种语言的所有词汇。为了简单方便起见，我们只选择了一小部分词汇。

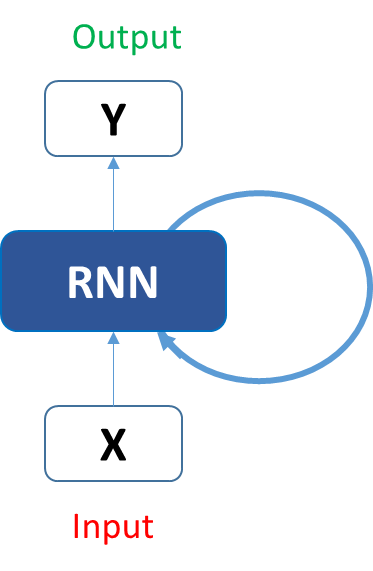
让我们看下上图中展示的结构是如何预测出‘hello’这个单词中的第五个字符。在上述结构中，蓝色RNN部分，使用一种循环公式，该公式结合当前输入向量和前一状态。在这个例子中，字符‘h’ 之前不包含任何字符，让我们看下字符‘e’。所以当将字符 ‘e’ 输入至网络中时，循环公式同时作用于当前字符‘e’和前一字符‘h’。这可以被认为是一个时间序列的输入。假设在时刻t，输入的字符为 ‘e’，那么t-1时刻的输入的字符为’h‘。这是循环公式同时作用于字符’e‘和’h‘，然后我们可以获得新的状态。

根据上面的描述，我们可以得到下述公式：

在这 是当前的状态， 是前一状态， 是当前输入。现在我们拥有的是前一输入的状态，而不单单只是前一输入本身。所以每一个连续的输入都被称为time step。

在这个例子中我们包含4个输入来传入神经网络，在这循环神经网络中，同样的函数和同样的权重被应用到网络中在每一个时间序列中。

我们假设循环神经网络中的激活函数为，假设循环神经元的权重参数为 ， 输入层的权重参数为 ，所以我们可以得到如下的公式：

在这个循环神经网络中只考虑了前一步的状态。对应长序列可能包含多层这样的状态，得到最后一个状态就是我们需要的输出。

一旦我们计算了当前的状态，我们可以通过下面的公式获得最后的输出结果

让我们总结下循环神经网络中每一步都是怎么处理的：

  1. 每一个时间周期将输入传输给网络，例如：
  2. 通过结合前一状态和当前输入来计算当前状态
  3. 当前状态 在下一轮迭代中变为前一状态
  4. 根据实际问题的需要，可以经过多个时间周期的循环，从而结合之前更多层的状态
  5. 一旦所有的循环迭代都完成，最终的当前状态可以用来计算最终的输出
  6. 预测结果与实际结果进行比较得到他们之间的误差
  7. 最后将误差反向传播会网络，并且更新相关神经元的权重。

4. 循环(递归)神经网络中的前向传播

让我们先看下相应的输入：

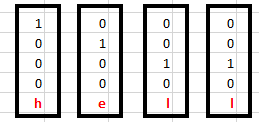
该输入采用的是one-hot编码模式，我们整个词汇表只有{‘h’, ‘e’, ‘l’, ‘o’}，所以我们可以很简单的使用one-hot编码来编码输入。

那么输入层神经元可以通过权重 将输入转换成隐藏状态。我们随机初始化一个 的权重矩阵。

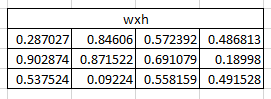
Step 1

对应字符’h’，我们可以采用来获取隐藏状态，如下所示：

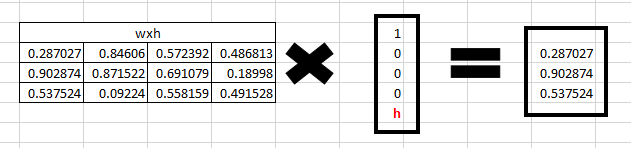
Step 2

紧接着进入循环神经元，我们有权重 是一个 的矩阵 [0.427043]， 同时偏移量为 矩阵 [0.56700]。

对应字符 ’h‘, 前一状态为 [0, 0, 0]，因为之前没有任何字符存在。

所以通过公式 计算：

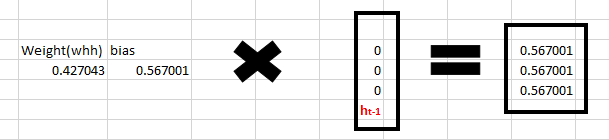
Step 3

那么我们可以通过如下公式计算当前状态：

对应字符 ’h‘ 没有前一状态，所以我们将函数 直接作用于 ，那么我们就能得到当前状态

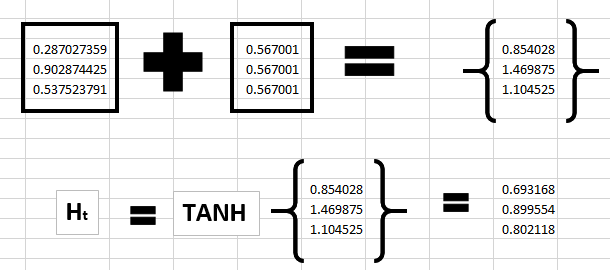
Step 4

接下来我们进入下一个阶段。我们将 “e”输入网络中，来获取当前状态 根据字符的one-hot编码和前一状态 我们可以得到：

的计算结果将为：

的计算结果为：

Step 5

接下来，让我们计算字符 ‘e’ 的状态

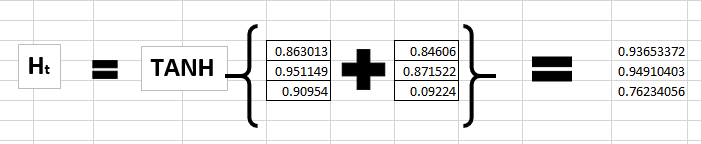
紧接着会变成 对应不断的输入来说。

Step 6

在每一步状态中，循环神经网络都会计算出一个输出，我们以字符 ‘e’的输出 ‘y_{t}’

Step 7

计算不同字符的概率值，我们采用softmax函数来进行计算

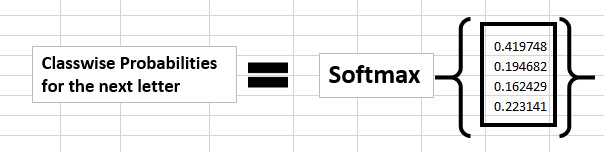
如果我们将这个概率转换成我们可以理解的预测，我们可以看到在字符 ’e‘ 之后是字符 ’h‘ 的概率要高一些。这是不是意味着我们计算出错了？不，因为我们只训练了两个字符。

那么紧接着比较严重的问题是后向传播算法是如何计算的呢？

5. 循环(递归)神经网络中的后向传播

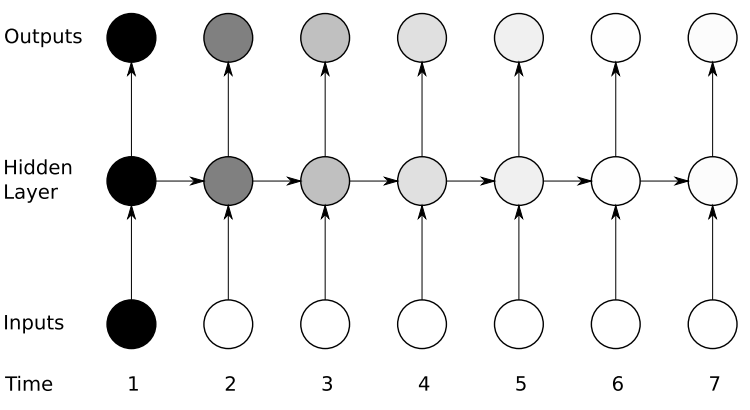
在循环神经网络中我们该怎么更新权重，这也许会存在一些挑战。为了让我们更好的理解后向传播算法，我们将网络每一步用图展示下。在RNN中我们有可能并不是每一步都会有输出。

在前向传播中，输入数据并且每一次向前移动一步。在这我们每计算一步都会方向更新下权重，我们将它称之为基于时间的方向传播( Back propagation through time BPTT)

在本例的RNN中，如果 是预测值， 是实际的结果值，我们通过交叉熵损失函数：

我们将一整个单词作为一个训练样本，所以总的错误就是每一步(字符)的错误之和。如我们所知，每一步使用到的权重参数是一样的。让我们总结下后向传播的：

  1. 交叉熵误差是通过计算的是当前预测输出结果和实际结果之间的误差
  2. 请记住，网络在所有时间步骤中都是展开的
  3. 对于这个展开网络，相对于权重参数不同的是我们计算每一个时间步骤的梯度
  4. 现在每一步中权重参数是一样的，同时各步得到的梯度可以结合在一起
  5. 最后循环神经元和dense layer的权重一起更新

展开的网络跟普通的神经网络比较类似，同理后向传播算法也是跟普通神经网络是类似的，只不过是我们结合了所有时间步的梯度。那么你可以想象下，如果一个包含一百多步的循环神经元。如果我们将网络展开的话我们将花费非常长的时间才能使得网络收敛。

在这我们就不对后向传播算法的数学推导进行详细的描述。

6. 梯度消失和爆炸问题

RNN的工作原理是一个结果的计算是依赖前一个结果的状态甚至是前n步的状态。对于普通的RNN应用于长距离的状态依赖是非常困难的事情。例如：我们有个句子 “The man who ate my pizza has purple hair”.在这个例子中，purple hair 是用来描述人的而不是用来描述pizza的。

以我们上述例子来说，如果我们需要计算交叉熵误差的反向传播，我们将需要采用链式法则，

在这我们使用链式法则来进行后向传播，假设其中一个梯度计算出来等于零或者接近于零。由于乘法的原因会导致最终的结果为零。这样对于整个网络的学习是不利的，因为学习不到任何知识。这就是通常我们说的梯度消失问题。

相比由于单个或者多个梯度值变得非常高，梯度变得非常大引起的梯度爆炸，梯度消失对整个网络的学习更加的不利。

相比梯度消失，梯度爆炸可以通过设定一个阈值来限制梯度的大小，从而解决梯度爆炸的问题。不过值得庆幸的是，同样也存在一些方法能够解决梯度消失的问题。例如LSTM(long term short term memeory), GRU(Gated Recurrent Unit) 可以用来解决梯度消失的问题。

7. 其他的循环神经网络

正如我们所见的，对于长依赖的情形下，RNN会遇到梯度消失的问题。随着参数数量的变大，它们也变得更加难以训练。如果我们将网络展开，整个网络会变的非常的大，从而导致整个训练很难最终收敛。

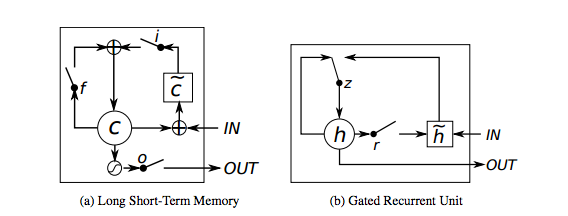
长短时记忆模型，通常称为LSTM，是一种特殊的RNN模型，能够用来训练长距离的依赖。该模型在适用于不同的问题，并且现在得到了比较广泛的应用。LSTM具有相同的链式结构，但是模型中循环组件存在一定的不同。相比于传统的RNN模型只有一层神经元，LSTM拥有多层神经元，并且这些层神经元采用一些特殊的交互方式进行交互。其中包含了输入门(input gate), 输出门(output gate), 还有一个忘记门(forget gate)。

另外一个类RNN模型是Gated Recurrent Units(GRU)，它是LSTM的变种，但是具有更简单的结构，并且训练会更加方便。

8. 参考文献

9. 附录

9.1 使用Keras来实现RNN

让我们使用RNN来预测不同推文的表达的情绪。具体代码请见tweet_sentiment.py

Related Posts