生成训练和测试数据集
我们在这使用新的数据集,Wine数据集,该数据集可以从UCI机器学习库中获取。
import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data')
df_wine.cloumns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols', 'Flavanoids',
'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue',
'OD280/OD315 of diluted wines','Proline']
print('Class labels', np.unique(df_wine['Class label']))
('Class labels', array([1, 2, 3]))
该数据集包含172个样本,每个样本有13个酒化学特征
df_wine
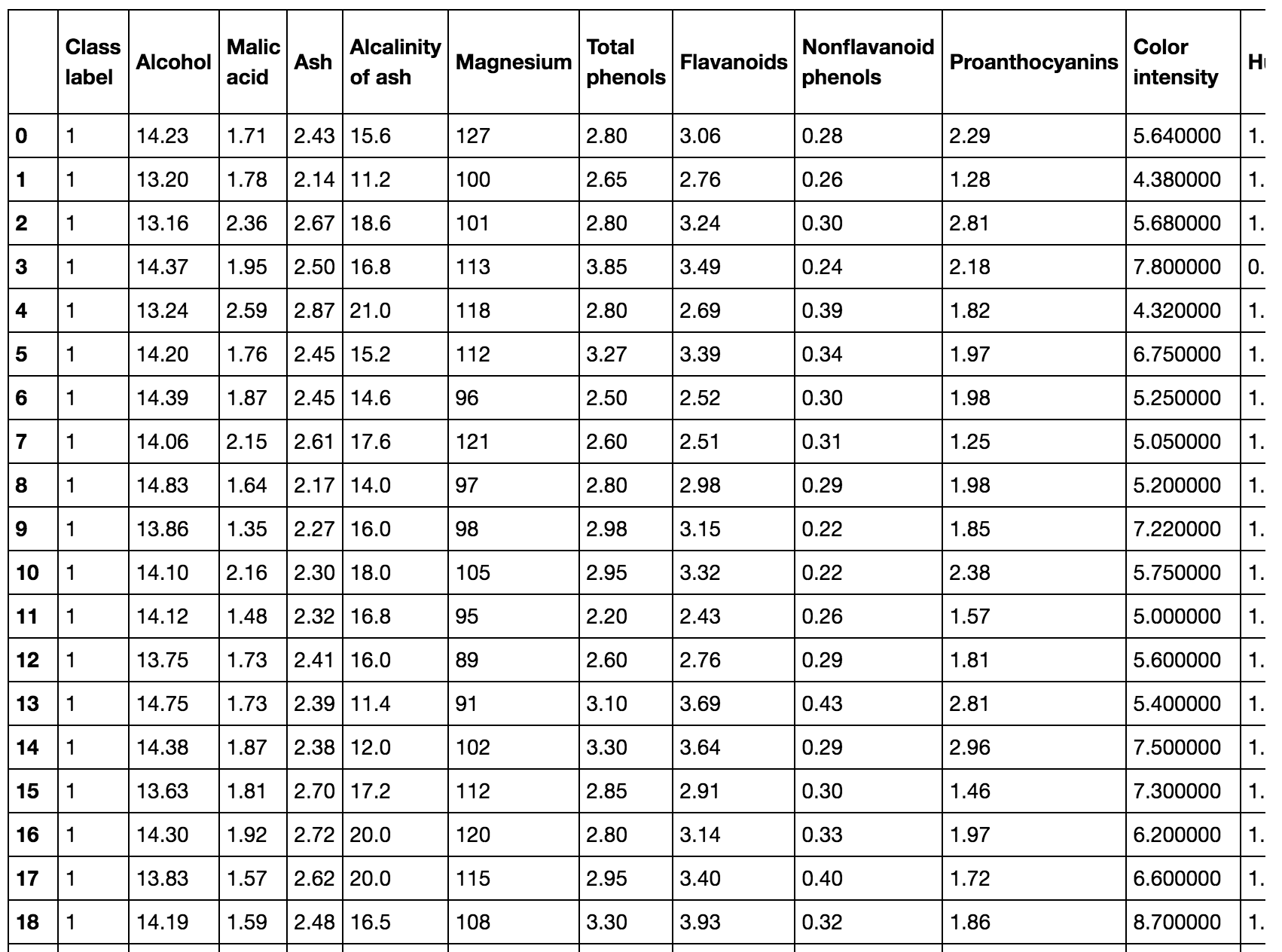
df_wine.head()
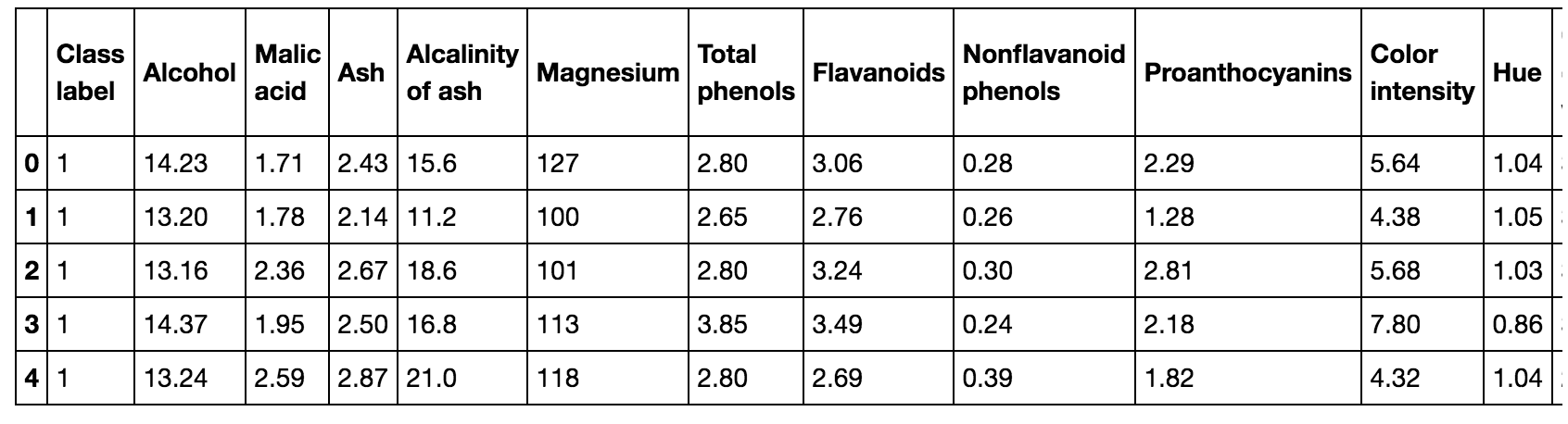
每个样本隶属于三种不同类型1, 2,3 中的一种。三种类型样本的区别主要在于意大利不同地区生长的不同葡萄类型。
我们可以使用scikit-learn cross_validation模块中的 train_test_split() 函数,来将样本集随机的分解成训练集和测试集。
df_wine.iloc[:, 0].values
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3])
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3, random_state=0)
从上述代码中,我们将1-13列的特征赋给了, 将类别赋给了 。 然后我们使用函数 train_test_split() 将 和 随机分解成训练集和测试集。
其中设置参数 test_size=0.3 表示将30%的样本划归为测试集 X_test, y_test, 剩下的70%样本为训练集 X_train, y_train。
len(X_test), len(X_train)
(54, 124)
特征缩放(feature scaling)
特征归一化是一种用于标准化特征范围的方法。是数据预处理中关键的一步。
假设我们有两种特征,一种特征的范围从0到1, 另一种特征的范围从1到100。当我们在计算k最近邻的平方误差或者欧氏距离时,第二种特征将会带来比较大的影响。
通常,归一化是通过某种映射关系,将特征值的范围缩放值[0, 1] 之间。
我们可以使用min-max scaling方法来缩放不同的特征。其中归一化后的值 可以通过下面的方式获得:
让我们看下使用scikit-learn如何实现:
from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler()
X_train_norm = mms.fit_transform(X_train)
X_test_norm = mms.transform(X_test)
X_train_norm[0]
array([ 0.72043011, 0.20378151, 0.53763441, 0.30927835, 0.33695652, 0.54316547, 0.73700306, 0.25 , 0.40189873, 0.24068768, 0.48717949, 1. , 0.5854251 ])
X_test_norm[0]
array([ 0.72849462, 0.16386555, 0.47849462, 0.29896907, 0.52173913, 0.53956835, 0.74311927, 0.13461538, 0.37974684, 0.4364852 , 0.32478632, 0.70695971, 0.60566802])
通过 min-max scaling 归一化(normalization)可以将特征值的值域限定在一定范围内, 如果我们希望标准化后的特征能满足正态分布,那么可以使用特征标准化(standardized),相比使用min-max归一化算法,特征标准化会更不易受离群点的影响:
其中 对应的是某列特征值的均值, 对应特征值的标准差。
下表展示了min-max特征归一化算法和特征标准化(standardized)之间的区别
| input | standardized | normalized |
|---|---|---|
| 0.0 | -1.336306 | 0.0 |
| 1.0 | -0.801784 | 0.2 |
| 2.0 | -0.267261 | 0.4 |
| 3.0 | 0.267261 | 0.6 |
| 4.0 | 0.801784 | 0.8 |
| 5.0 | 1.336306 | 1.0 |
让我们看下特征标准化在scikit-learn中是如何实现的
from sklearn.preprocessing import StandardScaler
stdsc = StandardScaler()
X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.transform(X_test)
X_train_std[0]
array([ 0.91083058, -0.46259897, -0.01142613, -0.82067872, 0.06241693, 0.58820446, 0.93565436, -0.7619138 , 0.13007174, -0.51238741, 0.65706596, 1.94354495, 0.93700997])
下面是特征标准化和特征归一化之间的对比:
xx = np.arange(len(X_train_std))
yy1 = X_train_norm[:,1]
yy2 = X_train_std[:,1]
scatter(xx, yy1, color='b')
scatter(xx, yy2, color='r')
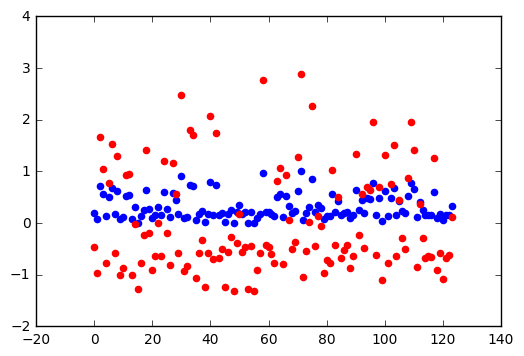
特征选择(feature selection)
当我们如果遇到模型在训练数据上的表现要比在测试数据集上好很多的情况, 我们就要考虑到是不是因为过拟合(overfitting)或者模型方差过大(high variance)。
换句话说,我们训练得到的模型参数对训练数据描述的过于接近,从而导致模型的泛化性不足。
下面有些减少模型泛化错误的方法:
- 选择一个简单模型,该模型拥有较少的参数
- 通过正则化惩罚方法来降低模型的复杂度
- 降低数据的维度
- 尽量收集更多的训练样本,不过这种方法可操作性较低。
正则化(regularization)
正则化是一种调整和选择模型复杂度的优先考虑的方法,从而能让模型获得更好的预测效果。
如果我们不做正则化,我们的模型也许不能获得很好的泛化性当模型对训练数据描述的非常好。
正则化引入了对大权重的惩罚,以便我们可以降低模型的复杂性。
我们可以使用两种正则化方法:L1 和 L2
与L2正则化不同,L1正则化更容易产生稀疏特征向量,因为大多数特征权重将为零。
当我们拥有一个具有许多不相关特征的高维数据时,稀疏性在实际应用中还是非常有用。
正如这样,L1正则化可以用来做特征选择
L1 正则化 和稀疏解决方案
我们希望在数据(非成本函数)和正则化(惩罚或偏差)之间取得平衡。
(1)
解如下:
(2)
通过正则化参数λ,那么我们就可以控制模型在保证权重值小的前提下,更好的适应训练数据
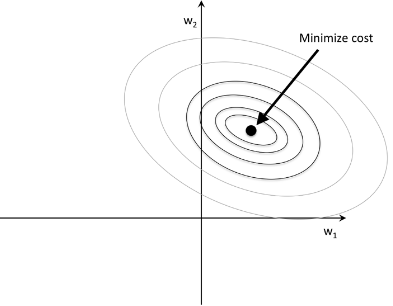
我们的主要目标是找到最小化训练数据成本函数的权重系数组合。
正如公式(1) 所示,我们在损失函数后面增加了一个正则化项,这样可以让我们获得更小的权重
通过增加正则项,从而增加正则化的强度,从而收缩模型的权重值,从而降低模型对训练数据的依赖。
对于L2正则化,下图直观展示了相关的处理逻辑,其中阴影部分为L2项
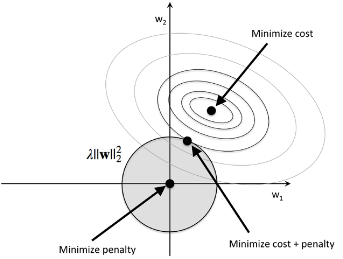
在这模型的权重系数不能超出正则项范围的限制 budget(C)
换句话说,我们不仅需要保证损失较少,同时也要保证权重系数不能超出阴影部分。
接下来我们来看下 L1正则化
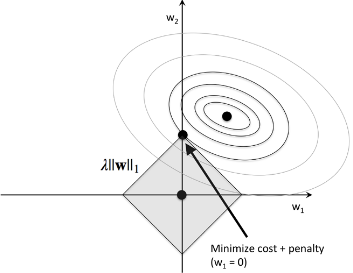
正如上图展示的,L1正则化使得某一个权重值取零。从而相比 L2正则化,L1正则化更容易产生稀疏性。
scikit-learn 中的L1正则
让我们看下在scikit-learn中是如何支持 L1正则的
from sklearn.linear_model import LogisticRegression
LogisticRegression(penalty='l1')
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=100, multi_class=’ovr’, n_jobs=1, penalty=’l1’, random_state=None, solver=’liblinear’, tol=0.0001, verbose=0, warm_start=False)
L1正则化表现
让我们使用图像直观的展示下,在不同惩罚强度下,不同特征的模型权重参数的变化
fig = figure()
ax = subplot(111)
colors = ['blue', 'green', 'red', 'cyan',
'magenta', 'yellow', 'black',
'pink', 'lightgreen', 'lightblue',
'gray', 'indigo', 'orange']
weights, params = [], []
for c in np.arange(-4, 6):
lr = LogisticRegression(penalty='l1',
C=10**c, random_state=0)
lr.fit(X_train_std, y_train)
weights.append(lr.coef_[1])
params.append(10**c)
weights = np.array(weights)
for column, color in zip(range(weights.shape[1]), colors):
plot(params, weights[:, column],
label=df_wine.columns[column+1], color=color)
axhline(0, color='black', linestyle='--', linewidth=3)
xlim([10**(-5), 10**5])
ylabel('weight coefficient')
xlabel('C')
xscale('log')
legend(loc='upper left')
legend(loc='upper center',
bbox_to_anchor=(1.38, 1.03),
ncol=1, fancybox=True)
show()
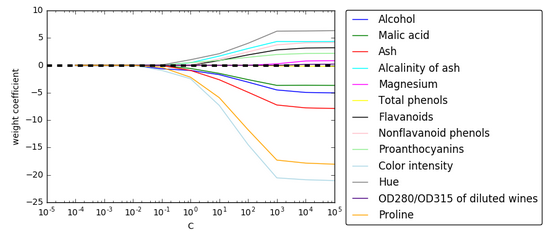
从上图可知,当惩罚因子 越大的时候,会导致更多的特征权重接近 0。