主成分分析(Principal Component Analysis)
主成分分析(Principal Component Analysis,PCA), 是一种统计方法。通过正 交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分
PCA 顾名思义主要是通过找到数据集的方差最大方向(正交轴方向/主成分),并且将原数据投射到新的主成分子空间中,从而降低数据的维度。
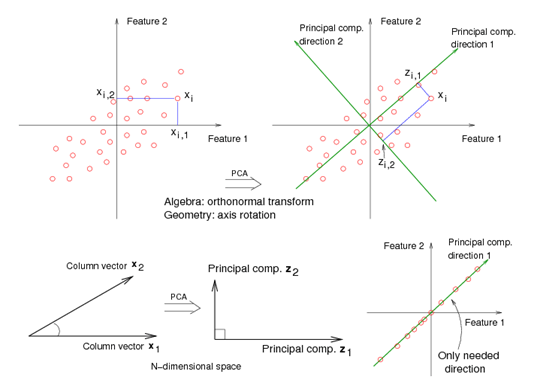
其中 和 是原来的特征轴, 和 是主成分方向。
通过主成分分析对特征进行降维
为了能够使用PCA对特征进行降维,我们将构建一个转换矩阵 它的是 维的矩阵。
通过转换矩阵 我们将每个样本向量 映射到一个 维的子空间中,这样就将原来的d维向量降低成了 k 维向量。
需要注意的是PCA 对数据大小比较敏感,所以我们在使用PCA前,最好先对不同的特征做特征归一化处理。
下面是使用PCA做特征降维的操作步骤:
- 标准化d维特征数据集(数据归一化)
- 构建协方差矩阵
- 将协方差矩阵分解出它的特征向量和特征值
- 选出其中k个最大特征值对应的特征向量,其中 是新子空间的维度()
- 通过 个特征向量构建出相应的转换矩阵
- 通过转换矩阵 将原 维特征向量转换成 维特征向量。
特征值和特征向量
紧接上节中说明的主成分分析。在这节中,我们将对特征数据进行标准化,构建协方差矩阵,计算协方差矩阵的特征向量和特征值,对特征值进行排序,并选择其中最大的 个特征值对应的特征向量。
import pandas as pd
df_wine = pd.read_csv(
'https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',
header=None)
df_wine.head()
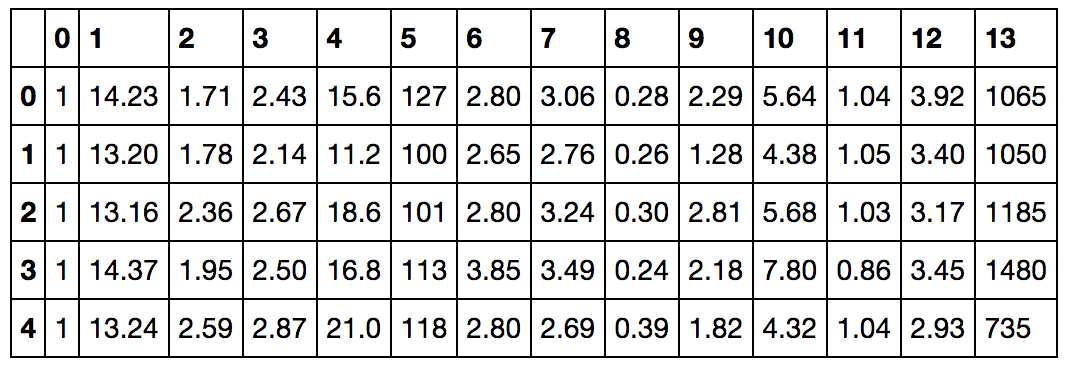
其中 PCA 是无监督学习,也就是样本对应的标签数据信息是不被考虑的。与随机森林对特征进行降维的方法不同的是PCA更多利用特征值之间的关系。
接下来我们展示如何使用scikit-learn 做PCA 操作
首先将数据读入,并将70%的数据划归为训练集,30%的数据集划归为测试集,并对这些特征进行特征标准化操作
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3, random_state=0)
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)
接下来我们需要构建 维协方差矩阵,其中 是数据集的大小。该协方差矩阵存放了不同特征向量之间的协方差。
特征向量 和 的协方差可以通过以下的公式进行计算:
其中 和 是特征 和 的样本均值
三个特征向量对应的协方差矩阵如下:
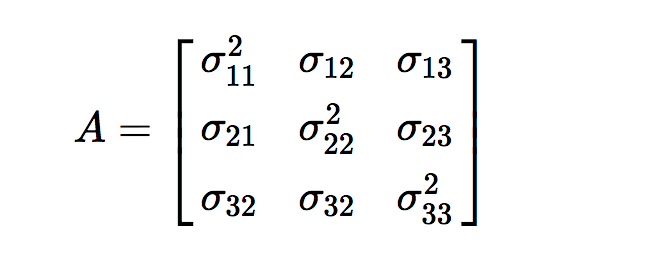
协方差矩阵的特征向量表示了主成分,其中对于的特征值定义了主成分的等级
在 Wine 数据集中,我们从 的协方差矩阵中,计算得到了13个特征向量和特征值。
其中特征向量满足下面的公式, 其中 是特征值:
我们可以使用 Numpy 包中的 linalg.eig 函数来获取Wine协方差矩阵对应的特征向量:
covariant_matrix = np.cov(X_train_std.T)
covariant_matrix[0::5]
array([[ 1.00813008, 0.08797701, 0.23066952, -0.32868099, 0.2141631 ,
0.35576761, 0.2991246 , -0.16913744, 0.09649074, 0.56962271,
-0.04781543, 0.07403492, 0.63277882],
[ 0.35576761, -0.30124242, 0.12235533, -0.37018442, 0.16513295,
1.00813008, 0.88119961, -0.45396901, 0.6196806 , -0.06935051,
0.45718802, 0.72214462, 0.56326772],
[-0.04781543, -0.54992807, -0.10928021, -0.25313262, 0.05792599,
0.45718802, 0.58331869, -0.3178224 , 0.32282167, -0.52395358,
1.00813008, 0.60022569, 0.2452794 ]])
eigen_values, eigen_vectors = np.linalg.eig(covariant_matrix)
eigen_values, eigen_vectors[::5]
(array([ 4.8923083 , 2.46635032, 1.42809973, 1.01233462, 0.84906459,
0.60181514, 0.52251546, 0.08414846, 0.33051429, 0.29595018,
0.16831254, 0.21432212, 0.2399553 ]),
array([[ 1.46698114e-01, 5.04170789e-01, -1.17235150e-01,
2.06254611e-01, -1.87815947e-01, -1.48851318e-01,
-1.79263662e-01, -5.54687162e-02, -4.03054922e-01,
-4.17197583e-01, 2.75660860e-01, 4.03567189e-01,
4.13320786e-04],
[ 3.89344551e-01, 9.36399132e-02, 1.80804417e-01,
1.93179478e-01, 1.40645426e-01, 1.22248798e-02,
5.31455344e-02, -4.21265116e-01, 1.35111456e-01,
-2.80985650e-01, 2.83897644e-01, -6.18600153e-01,
9.45645138e-02],
[ 3.00325353e-01, -2.79243218e-01, 9.32387182e-02,
2.41740256e-02, -3.72610811e-01, 2.16515349e-01,
-3.84654748e-01, -1.05383688e-01, -5.17259438e-01,
1.97814118e-01, -1.98844532e-01, -2.00456386e-01,
-3.02254353e-01]]))
我们通过 numpy.cov 来计算标准化后的训练集的协方差矩阵
使用 linalg.eig 函数来计算 协方差矩阵对应的特征值和特征向量。
因为我们想将训练数据集的特征维度降低到一个新的子空间中,所以我们只选择包含最多信息的特征向量。
因为不同特征值大小反应了对应特征向量的重要性,所以我们对特征值做降序排序,并取出其中排在前的 个特征向量。
在我们取出其中 个特征向量前,让我们通过特征值的比率来看看不同特征之间的方差
tot = sum(eigen_values)
var_exp = [(i / tot) for i in sorted(eigen_values, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
bar(range(1,14), var_exp, alpha=0.5, align='center',
label='individual explained variance')
step(range(1,14), cum_var_exp, where='mid',
label='cumulative explained variance')
ylabel('Explained variance ratio')
xlabel('Principal components')
legend(loc='best')
show()
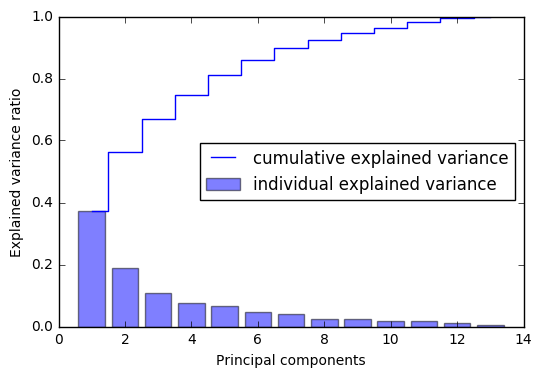
从图中我们可以看出,第一个主成分蕴含了40%的方差信息,前两个主成分包含了60%的方差信息。
将数据集映射到新的坐标系
接下来,我们将选择出前 个特征向量,并将原数据集映射至新的特征子空间中
eigen_pairs = \
[(np.abs(eigen_values[i]),eigen_vectors[:,i]) for i in range(len(eigen_values))]
eigen_pairs.sort(reverse=True)
eigen_pairs[:5]
[(4.8923083032737509,
array([ 0.14669811, -0.24224554, -0.02993442, -0.25519002, 0.12079772,
0.38934455, 0.42326486, -0.30634956, 0.30572219, -0.09869191,
0.30032535, 0.36821154, 0.29259713])),
(2.4663503157592306,
array([ 0.50417079, 0.24216889, 0.28698484, -0.06468718, 0.22995385,
0.09363991, 0.01088622, 0.01870216, 0.03040352, 0.54527081,
-0.27924322, -0.174365 , 0.36315461])),
(1.4280997275048455,
array([-0.11723515, 0.14994658, 0.65639439, 0.58428234, 0.08226275,
0.18080442, 0.14295933, 0.17223475, 0.1583621 , -0.14242171,
0.09323872, 0.19607741, -0.09731711])),
(1.0123346209044966,
array([ 0.20625461, 0.1304893 , 0.01515363, -0.09042209, -0.83912835,
0.19317948, 0.14045955, 0.33733262, -0.1147529 , 0.07878571,
0.02417403, 0.18402864, 0.05676778])),
(0.8490645933450266,
array([-0.18781595, 0.56863978, -0.29920943, -0.04124995, -0.02719713,
0.14064543, 0.09268665, -0.08584168, 0.56510524, 0.01323461,
-0.37261081, 0.08937967, -0.21752948]))]
接下来我们选择前两个蕴含了60%变化的特征向量
w= np.hstack((eigen_pairs[0][1][:, np.newaxis], eigen_pairs[1][1][:, np.newaxis]))
w.shape
(13, 2)
w
array([[ 0.14669811, 0.50417079],
[-0.24224554, 0.24216889],
[-0.02993442, 0.28698484],
[-0.25519002, -0.06468718],
[ 0.12079772, 0.22995385],
[ 0.38934455, 0.09363991],
[ 0.42326486, 0.01088622],
[-0.30634956, 0.01870216],
[ 0.30572219, 0.03040352],
[-0.09869191, 0.54527081],
[ 0.30032535, -0.27924322],
[ 0.36821154, -0.174365 ],
[ 0.29259713, 0.36315461]])
现在我们得到了一个 的转换矩阵
接下来我们使用该转换矩阵,将每个样本 () 映射成一个二维向量
X_train_std[0]
array([ 0.91083058, -0.46259897, -0.01142613, -0.82067872, 0.06241693,
0.58820446, 0.93565436, -0.7619138 , 0.13007174, -0.51238741,
0.65706596, 1.94354495, 0.93700997])
X_train_std[0].dot(w)
array([ 2.59891628, 0.00484089])
同理,我们可以将整个 的训练数据集通过矩阵点乘将所有样本都映射到二维空间中
X_train_pca = X_train_std.dot(w)
X_train_std.shape, w.shape, X_train_pca.shape
((124, 13), (13, 2), (124, 2))
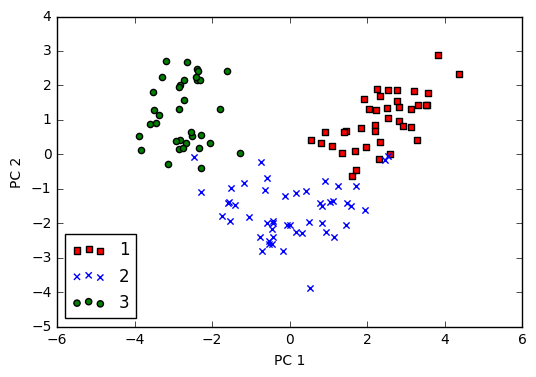
最后我们图示下最终的124个样本在二维空间的分布
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
scatter(X_train_pca[y_train==l, 0], X_train_pca[y_train==l, 1],
c=c, label=l, marker=m)
xlabel('PC 1')
ylabel('PC 2')
legend(loc='lower left')
show()
scikit-learn PCA 实现
在这节中我们将展示如何使用scikit-learn 中的PCA
如下代码所示:
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
xlim(xx1.min(), xx1.max())
ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
lr = LogisticRegression()
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
lr.fit(X_train_pca, y_train)
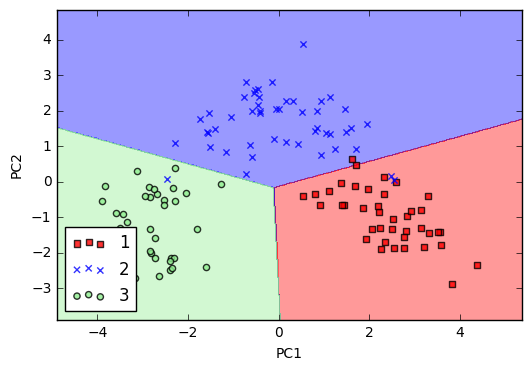
plot_decision_regions(X_train_pca, y_train, classifier=lr)
xlabel('PC1')
ylabel('PC2')
legend(loc='lower left')
show()